JavaScript中的数字存储

发表于 | 分类于 | 阅读次数:
字数统计: 3,373 | 阅读时长 ≈ 13

JavaScript中数字是不区分整数值与浮点数值的，在JavaScript中所有的数均使用64位的浮点格式来存储和表示（IEEE 754标准）。所以数值最大是：±1.7976931348623157 X 10^308，最小是±5X10^-324，可以表示的整数范围是-9 007 199 254 740 992 ~ 9 007 199 254 740 992 （对应的是-2^53~2^53）包含边界值。

注意这里说的最大/小，准确的应该说是：在正数和负数范围内可以准确得到的最大最小的数
比如1.7976931348623157 X 10^308 是可以得到的最大的正数，也就是 JavaScript 中的MAX_VALUE，任何大于这个的在 js 中都是 Infinity，需要注意的是，他的负数，从数学上可以说是最小值，但是在存储上并不是最小的值
而 5X10^-324 是可以得到的最小的 最接近于 0 的最小的值，js 中的 MIN_VALUE 的值约为 5e-324。小于 MIN_VALUE (“underflow values”) 的值将会转换为 0， 注意，当这个数值表示为负数的时候 他是负数范围内最大的数值

注意了啊，上面的有隐藏的问题的，结尾有相关的解释哈

注意：在对JS中的数值进行位操作的时候会自动把64位转化为32进行操作（由于运算符的自身限制，其只能对32位进行操作），在对小数进行位操作 比如左移零位，小数会丢弃小数部分转化成整数, 所以以后看到 1.25 >> 0，就知道大佬是想做一个取整操作啦 这里尤其注意的一点通过位运算来做取整操作，会有溢出风险，数值会变，所以请谨慎使用 。


JavaScript中数字不一定很准确

首先我们先看一段代码

1
2
3
4
5
6
var x = 0
var y = 0
x = .3 - .2
y = .2 - .1
console.log(x == .1 ) // false
console.log(y == .1 ) // true

运行结果是 false 和 true
讲道理的说0.3 - 0.2 = 0.1;0.2-0.1 = 0.1 这个是正确的，那么为什么到了JS的代码里就不正确了，解决这个问题，我们首先要看一下JS的数字是如何存储的。

基础知识点补充 进制的转换

JS数字的存储

在本文的前言中我们说到了JS用的是IEEE754标准，这个标准规定了浮点数的表示方法（此方法也是目前通用计算机所才用的浮点数存数方式）。在此标准中浮点数有float和double两种存储形式，但是JS的数字只采用了double类型来做存储，也就是我们常说的使用64位来存储数字的双精度型。那么我们是如何利用这64位来存储数据的呢？ 我们都知道科学计数法，即把一个数比如123465.555可以写成1.23456555*10^5，这样子不仅读写方便也能减少存储该数字的空间，123456.555是一个十进制的数字，那么我们是把一个二进制的数字是否也可以转化成这个形式，以达到减少存数空间的目的，答案是肯定的。我们把一个十进制数比如：16.25 写成二进制的形式：10000.01，类比十进制的写法，我们可以把他写成 1.000001X2^4，现在我们看一下这个数字，他由有效数字 1.000001 以及指数 2^4 以及我们省略了的符号位组成（正数的符号位是 + 负数的是- 零的话严格来说不属于正负，计算机如何处理他我们后文将解释），那么64位的空间我们就知道需要放三大块的东西了：有效数字、指数、符号位

  • sign bit(符号)：我们在64位的最高位放置符号位，最高位为1，表示数字是正数还是负数
  • exponent(指数): 我们在从左往右再取11位用来表示指数
  • mantissa(尾数): 我们把剩余的52位空间全部用来存储有效数字

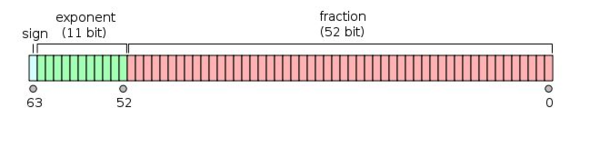
    1.为了最大限度的利用存储有效数字的52位，我们把小数点以及小数点前的那一个数字给省略掉（正确的化简后尾数会被处理到大于等于1而小于2的区间内，这时候便可省去前导的“1”），所以我们只需要存贮小数点后面的 000001就可以了
    2.在上图中存储指数的数值叫做阶码，有它转换出来的阶码的数值等于指数的数值，阶码=指数+1023 (科学计数法中的指数是可以为负数的，所以约定减去一个中间数 1023，[0,1022] 表示为负，[1024,2047] 表示为正)。在 ECMAScript 规范里有给出指数的范围： [-1074, 971] 。

    为什么会出现数字不准确

    现在我们知道了一个数是如何存储的，那么我们来想一个问题，1.3 转化为二进制是多少0.010011001100....1100，对的你发现了他的小数部分除不尽，那么意味着他的小数部分用64位表示不完。我们来看一下浏览器是如何处理的。
    1
    2
    var a = 1.3
    console.log(a.toString(2))
    输出的结果是 1.010011001100110011001100110011001100110011001100110011
    我们来比较一下浏览器计算的1.3和我们手算的1.3的差别
    1
    2
    浏览器： 1.0100110011001100110011001100110011001100110011001101
    手 算 ： 1.0100110011001100110011001100110011001100110011001100*1100*

我们看到浏览器进行了进位操作，浏览器执行的是满1进位，不满则省略的方案
所以这也就是为什么我们在进行浮点数运算的时候有时得不到精确的数值的原因所在了。

为什么 0.3 == 0.3

1
2
var x = 0.3
console.log( x === 0.3 )

它的运行结果是true
前面不是说使用浮点数存储，小数部分出现循环后，系统存的不是一个准确数值，那么这里为什么会是true呢？
因为 尾数(mantissa) 固定长度是 52 位，再加上省略的一位，最多可以表示的数是 2^53=9007199254740992，对应科学计数尾数是 9.007199254740992，这也是 JS 最多能表示的精度（也就是说按照52个尾数全为0到其全为1，让其对应以十进制表示的从1到9007199254740992 注意我们省略了小数点前面的一位，所以计算的时候应该按照53位计算）。它的长度是 16，所以可以近似使用 toPrecision(16) 来做精度运算，超过的精度会自动做凑整处理。于是就有 x.toPrecision(16) === 0.3

toPrecision(16) 是先把二进制保存的不精确的那个数，转化为十进制数。然后是对十进制的数字再去保留小数点后的16位

大数危机

如果有数字处于2^53到2^63之间呢，他们是是如何取舍的

  • (2^53, 2^54) 之间的数会两个选一个，只能精确表示偶数
  • (2^54, 2^55) 之间的数会四个选一个，只能精确表示4个倍数…
  • 依次跳过更多2的倍数
    我们来看一张图（图是我偷得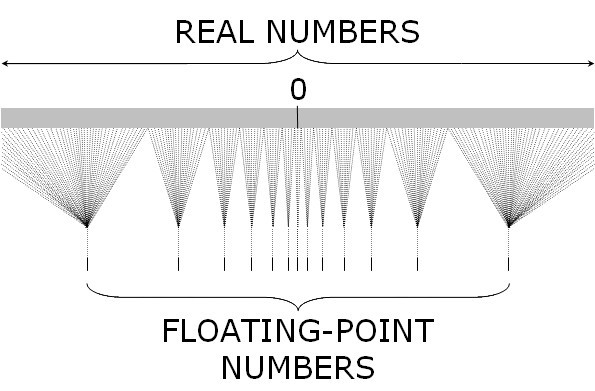） 我们可以看到在中间的部分，实数与浮点数还可以近似的一一对应，越往两边用浮点数与实数对应关系就越差，也就是说精度就逐渐的丢失

要想解决大数的问题你可以引用第三方库bignumber.js，原理是把所有数字当作字符串，重新实现了计算逻辑，缺点是性能比原生的差很多，所以原生支持大数就很有必要了。TC39 已经有一个 Stage 3 的提案proposal bigint，大数问题有望彻底解决。在浏览器正式支持前，可以使用Babel 7.0 来实现，它的内部是自动转换成 big-integer 来计算，这样能保持精度但运算效率会降低。

toPrecision 和 toFixed

  • toPrecision 是处理精度，精度是从左至右第一个不为0的数开始数起。
  • toFixed 是小数点后指定位数取整，从小数点开始数起。
    两者都能对多余数字做凑整处理，也有些人用 toFixed 来做四舍五入，但注意它是有坑的。
    比如1.055.toFixed(2) = 1.05 问题是他的第三位明明是5啊，说好的四舍五入呢？
    因为1.055实际对应的数字是1.0499999999 所以就出现前面的结果啦

    当你拿到 1.4000000000000001 这样的数据要展示时，建议使用 toPrecision 凑整并 parseFloat 转成数字后再显示。
    对于运算类操作，如 +-*/，就不能使用 toPrecision 了。正确的做法是把小数转成整数后再运算。
    ps:

    • 1.以上内容是原文章的删减内容，需要看原文章内容，下面有链接
    • 2.toPrecision 取一个经验数值 12 即可
    • 3.原文推荐了一个js处理浮点数的类库，大小只有1K，传送门: number-precision
    现在我们继续看这样一行代码
    1
    9999999999999999 == 10000000000000000

结果是true，这个又是为什么呢？
我们在前面说到e的范围是 [-1074, 971] ，也就是说他能保存的最大的数字是
1 x (2^53 - 1) x 2^971 = 1.7976931348623157e+308

  1. 52个1就等于 2^53 - 1
  2. 注意结果要补上我们省略的那个1.

类似的整数部分最小的是：1 x 1 x 2^(-1074) = 5e-324
由此我们可以知道：
Number.MAX_VALUE 以及 Number.MIN_VALUE 的两个数值了

注意：Number.MIN_VALUE 只是正数中最小的数字，实数最小的数字是 -Number.MAX_VALUE

现在结合前面所有的知识回过头来看一下，js中最大的数字是 Number.MAX_VALUE ，他是尾数为 2^53 指数为971 时候的数字
那么 如果有个数值他转成二进制的科学计数法之后，尾数大于2^53次方呢，这时候由于计算机会有一定的取舍（前文已经说过，具体的取舍方法有四条，有兴趣的可以自行维基解密），所以他的存储就有了误差。
所以经过了取舍的两个大数就相同了，

注意：其实现在我们可以发现在浮点数的时候虽然最大是 Number.MAX_VALUE，但是他有可能是其他的数值取舍得来，所以小于2^53的数值才是可以正确表示的数值，所以就有了 Number.MAX_SAFE_INTEGE 这个数值，其表示js中的安全数值

最后八卦几个数值

9007199254740990 (that is, 2^53-2) distinct “Not-a-Number” values of the IEEE Standard are represented in ECMAScript as a single special NaN value. (Note that the NaN value is produced by the program expression NaN.) In some implementations, external code might be able to detect a difference between various Not-a-Number values, but such behaviour is implementation-dependent; to ECMAScript code, all NaN values are indistinguishable from each other.

NAN = 9007199254740990 == 2^53−2 需要注意,NAN只是数值上是这个，但实际上他是有程序生成的所以所以NAN不等于NANHA

关于无穷大有个有意思的东西
首先抛出大佬给的问题（原始博文在最底部）

1
2
3
4
5
6
7
8
9
10
11
Number.MAX_VALUE + 1 == Number.MAX_VALUE;
Number.MAX_VALUE + 2 == Number.MAX_VALUE;
...
Number.MAX_VALUE + x == Number.MAX_VALUE;
Number.MAX_VALUE + x + 1 == Infinity;
...
Number.MAX_VALUE + Number.MAX_VALUE == Infinity;

// 问题：
// 1. x 的值是什么？
// 2. Infinity - Number.MAX_VALUE == x + 1; 是 true 还是 false ?

放出原博主的解答：

我的想法是这样的：

Number.MAX_VALUE.toString(16) = ”
fffffffffffff800000000000000000000000000000
00000000000000000000000000000000000000
00000000000000000000000000000000000000
00000000000000000000000000000000000000
00000000000000000000000000000000000000
00000000000000000000000000000000000000
00000000000000000000000″

前面有 13 个 f, 二进制就是 52 个 1
还有一个 8, 二进制是 1000
也就是说，前面 53 位都是 1

这样，当 Number.MAX_VALUE + 1 时，1 替代最后一个 0，但 IEEE 754 双精度浮点数的 m 最大为 53（含隐藏位），因此添加的 1 在存储时会被舍弃掉，所以：

Number.MAX_VALUE + 1 == Number.MAX_VALUE

同理类推，当 8（1000） 变成 b（1011），b 后面的位取最大值时，依旧有：

0xfffffffffffffbfffffffffffffffffffffffffffffffffffff
fffffffffffffffffffffffffffffffffffffffffffffffffffffff
fffffffffffffffffffffffffffffffffffffffffffffffffffffff
fffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffff == Number.MAX_VALUE

进一步，当 再增 1, b 变成 c 时，将发生质变：

0xfffffffffffffc00000000000000000000000000
000000000000000000000000000000000000
000000000000000000000000000000000000
000000000000000000000000000000000000
000000000000000000000000000000000000
000000000000000000000000000000000000
000000000000000000000000000000000000 == Infinity

这是因为前面将有 54 个连续的 1, 在存储时，exponent 将由
971 变成 972, 超出了 IEEE 754 双精度浮点数存储格式中 e 的
最大值，因此质变为 Infinity 了。

这样，题目中 x 的值就很容易得到了：

x = 0xfffffffffffffbffff… – 0xfffffffffffff80000…
= 0x00000000000003ffff…

注意这个数在IEEE 754 双精度浮点数格式下无法精确存储。

还能得到两个有趣的结论：

  1. Number.MAX_VALUE 不是一个数，而是一个区间 [0xfffffffffffff80000…, 0xfffffffffffffc0000…)
  2. Infinity 指的是，所有大于等于 0xfffffffffffffc0000… 的数。

更新一个 Number.EPSILON 知识点： Number.EPSILON 是 JS 里面 规定的 数值的最小精度，不是一个整数，是 它表示 1 与大于 1 的最小浮点数之间的差，

谢谢下面大佬指正

补充两个进制转换知识点吧，嗯，严格的来说是一个知识点，话不多说，直接上图

参考文档

  1. 谢大喵的上课视频
  2. 知乎：抓住数据的小尾巴 - JS浮点数陷阱及解法 https://zhuanlan.zhihu.com/p/30703042
  3. lifesinger的博客 https://lifesinger.wordpress.com/2011/03/07/js-precision/
  4. ECMAScript 规范 http://es5.github.io/#x8.5
  5. 进制转换 https://www.cnblogs.com/xkfz007/articles/2590472.html
感觉不错的话给博主赞助一下呗