牛顿法(英语:Newton’s method)又称为牛顿-拉弗森方法(英语:Newton-Raphson method),它是一种在实数域和复数域上近似求解方程的方法。方法使用函数 {\displaystyle f(x)} f(x)的泰勒级数的前面几项来寻找方程 {\displaystyle f(y)=0} {\displaystyle f(y)=0}的根。
再leetcode上看到这么一道题,题目很简单:1
2
3
4Sqrt(x)
Implement int sqrt(int x).
Compute and return the square root of x, where x is guaranteed to be a non-negative integer.
Since the return type is an integer, the decimal digits are truncated and only the integer part of the result is returned.
就是求一个数字的平方根,嗯题目没有截取完整们对于开方开出来是小数的,直接抛弃小数位(不是四舍五入)。
解题思路可以有很多,比较快的就是牛顿法了,一开始没有一下子想通牛顿法咋做,后来想通啦,所以就记录一下。
首先我们列一个关于被开方数z(在程序中是入口参数x)以及开放根x1的方程,x1 * x1 - z = y,我们把它记成F(x),当 y === 0 的时候说明x1为z的开放根。我们把他的图像画出来,图像如下(图是我从维基百科上偷得,自己的灵魂画图太丑了)
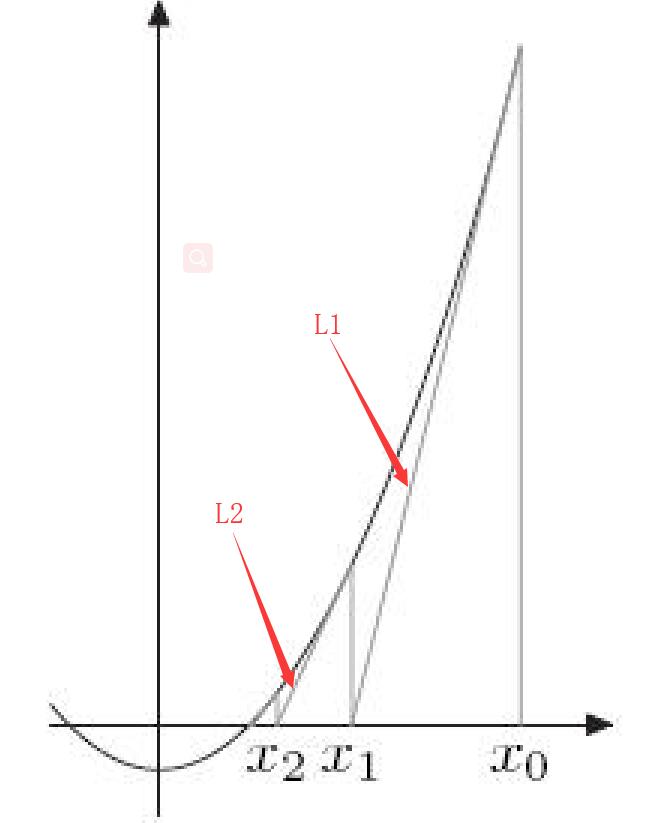
我们在x轴上找一点x0,过xo在F(x)的位置上做一条切线L1,我们可以看到L1与x轴的交点x1是逐渐逼近与F(x)与x轴的交点的,而这个交点也就是我们要求的开放根,然后我们继续做过x1在F(x)上的切线我们得到x2,不断的迭代下去,我们就可以得到一个符合我们要求的精确范围内的开放根。
现在我们需要用函数来写出来,我们想到了递归,但是想一下递归的空间复杂度,所以我们用循环来做,我们只需要不断的求x直到x满足要求的精度我们就跳出循环。
让我们来想一下我们如何通过现在的x来的出下一个x1呢?
我们看图像L1是F(x)在x0处的切线,那么这条切线的斜率就是F(x)的导函数在x0的结果。 现在我们这样子看一下1
2
3
4
5
6
7
8
9
10
11
12原函数F(x): x1 *x1 - z
原函数的导函数f'(x): 2 * x1
过x0的切线的方程我们设为:y = k*x + b
现在带入x0在此处的斜率和y
k = 2 * x0
y = x0 * x0 - z
我们得b = x0 * x0 - z - 2 * x0 * x0
所以得到x0的方程是 :
y = 2 * x0 * x + x0 * x0 - z - 2 * x0 * x0
= 2 * x0 * x - z - x0 * x0
我们可以看到,L1与x轴相交的点就是我们要求的x1,此时y = 0,所以x1 = (x0 * x0 + z)/ (2 * x0 * 10)
然后的出的x1不满足精确度,我们就把x1带入上面的式子,得出x2,然后不断迭代。代码如下1
2
3
4
5
6
7
8var mySqrt = function(x) {
var cout = 2
while (Math.abs(cout ** 2 - x) > 0.0000001) {
cout = (cout ** 2 + x) / (2 * cout)
}
return parseInt(cout)
};

